Extensive Form Representation in Game Theory

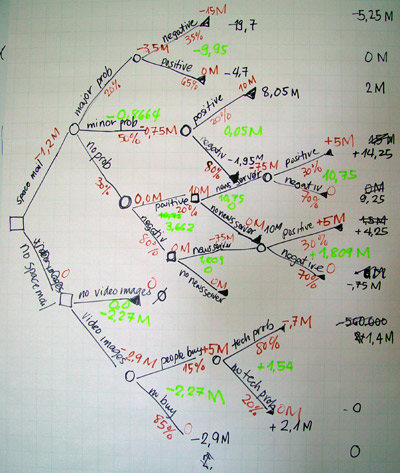
Decision support tool that uses a tree-like model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility.

In the realm of game theory, the extensive form is a way to describe a game that allows for the possibility of sequential moves. This form of representation is particularly useful when dealing with games where the order of moves matters, and it provides a more detailed view of the game's structure compared to the normal form representation.

Understanding Extensive Form Representation

The extensive form of a game is represented by a decision tree. Each node, or 'decision point', of the tree represents a point in the game where a player must make a decision. The branches that come out of these nodes represent the possible actions the player can take. The sequence of nodes and branches shows the order of moves, and the terminal nodes at the end of the branches represent the outcomes of the game.

Conversion of Normal Form Games to Extensive Form

While normal form games are represented in a matrix where each cell represents a possible outcome, they can be converted into extensive form for a more detailed analysis. This conversion involves identifying the sequence of moves and representing them as a decision tree. Each player's strategies are represented as paths in the tree from the root to a terminal node.

Decision Nodes and Branches

In the extensive form representation, decision nodes are typically labeled with the player who is making the decision at that point. The branches, or 'edges', represent the choices available to the player. Each decision node is connected to as many branches as there are available actions for the player. The complete path from the root to a terminal node represents a possible play of the game.

Information Sets and Perfect Information Games

An information set in a game is a collection of decision points where a player must make a move, but they cannot distinguish between these points based on the moves previously made. In other words, the player does not know which node within the information set they are at when they are making their decision.

In contrast, a game of perfect information is a game where all players know the moves previously made by all players. In the extensive form, a game of perfect information is represented by a tree where each player knows exactly where they are in the tree when making a decision.

In conclusion, the extensive form representation provides a detailed and sequential view of a game. It allows for a more nuanced analysis of games, especially those where the order of moves matters. By understanding this form of representation, players can better strategize and predict the outcomes of their decisions.